APLICACIONES DE LA DERIVADA(EQUIPO)

CBTF No. 6


TITULO:
APLICACIONES DEL CALCULO DIFERENCIAL:

ASIGNATURA: MATEMATICA APLICADA.



PROFESOR: MC. ROGELIO ORTEGA REYNOSO.



INTEGRANTES DEL EQUIPO:
CARLOS JAVIER GARCIA EVANGELISTA
EDITH HERREJON PIÑA
KARLA IVETH MORA AYALA
SOFIA CAMACHO GARCIA




FECHA: 22 ABRIL 2009.









INTRODUCCION

Cuando surgen cuestiones concernientes a la razón entre dos cantidades variables, entramos en los dominios del Cálculo Diferencial. Son por tanto objeto de estudio del cálculo diferencial temas como la velocidad (razón entre la distancia recorrida y el tiempo empleado en recorrerla) de una partícula en un momento determinado, la pendiente (razón entre la diferencia de las ordenadas y las abscisas de dos puntos en el plano cartesiano) de la recta tangente a una gráfica en un punto dado de ésta, etc.
Incrementos: cuando una cantidad variable pasa de un valor inicial a otro valor, se dice que ha tenido un incremento. Para calcular este incremento basta con hallar la diferencia entre el valor final y el inicial. Para denotar esta diferencia se utiliza el símbolo x, que se leee "delta x". El incremento puede ser positivo o negativo, dependiendo de si la variable aumenta o disminuye al pasar de un valor a otro. Por ejemplo, si el valor inicial de una variable x, x1, es igual a 3, y el valor final x2 es igual a 7, el incremento x = x2 - x1 = 7 - 3 = 4: la variable se ha incrementado positivamente en 4 unidades. En cambio, si el valor inicial es 7 y el valor final 3, x = x2 - x1 = 3 - 7 = -4: la variable ha tenido un incremento negativo (decremento) de 4 unidades.
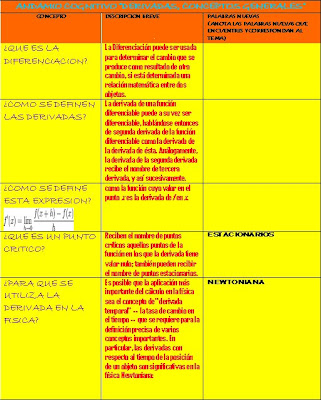
Derivada de una función: Sea f una función definida en todo número de algún intervalo I, la derivada de f es aquella función, denotada por f ', tal que su valor en cualquier número x de I, está dado por:

Se dice que una función es diferenciable o derivable cuando es posible hallar su derivada




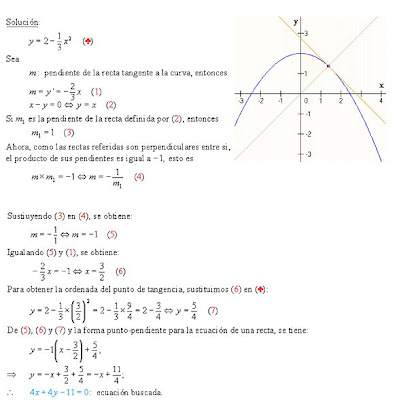
Obtenga una ecuación de la recta tangente a la curva que sea perpendicular a la recta

Solución:
(*)
sea:

m: pendiente de la recta pendiente a la curva, entonces

m = y´= (1)
(2)

Si m1 es la pendiente de la recta definida por (2), entonces

M1 = 1 (3)

Ahora como las rectas referidas son perpendiculares entre si,
el producto de sus pendientes es igual a -1, esto es:

Sustituyendo (3) en (4), se obtiene:


Igualando (5) y (1) se obtiene:


Para obtener la ordenada del punto de tangencia, sustituimos (6) en (*):


De (5), (6) y (7) y la forma punto-pendiente para la ecuación de una recta, se tiene:


ecuación buscada.




LOS INTEGRANTES DE ESTE EQUIPO SON: EDITH HERREJON PIÑA, KARLA IVETH MORA AYALA, SOFIA CAMACHO GARCIA Y POR SUPUESTO SU BROTHER CARLOS JAVIER GARCIA EVANGELISTA.
EXPERIENCIA DE EQUIPO: SE LLEGO A LA CONCLUSION DE QUE LA EXPERIENCIAQUE SE OBTUVO AL TRABAJAR DE ESTA FORMA FUE UNA BUENA IDEA QUE EXPERIMENTO EL PROFE, POR QUE EN PARTE APRENDIMOS LAS TECNICAS Y HERRAMIENTAS CON LAS QUE CUENTA EL SISTEMA DE COMPUTO COMO SON: CREAR UN BLOG EN LA WEB EL CUAL SERA MUY UTIL PARA DAR A CONOCER A LAS PERSONAS LOS ASPECTOS NO LOS MAS INPORTANTES QUIZA PERO LOO QUE NOSOTROS CONSIDERAMOS PUBLICAR, ADEMAS COMO YA LO MENCIONAMOS MEJORAMOS LAS TECNICAS DE COPIAR, CORTAR, PEGAR Y POR SUPUESTO ESCRIBIR DE UNA MANERA MAS RAPIDA Y EFICAZ. TODO ESTO ABARCA LA EXPERIENCIA OBTENIDA EN EL ASPECTO PARA LA FORMACION EDUCATIVA, LA OTRA PARTE DE ESTA FUE QUE MEJORAMOS LA AMISTAD Y EL COMPAÑERISMO DE TODO EL GRUPO PERO FUE MAYOR ENTRE NOSOTROS DEL EQUIPO.


REFERENCIAS DE DONDE SE TOMO LA INFORMACION:

1.http://es.wikipedia.org./wiki/Cáculo diferencial
2.http://es.wikipedia.org./wiki/Matem%Atica
3. http://es.wikipedia.org./wiki/Lógica matem%C3%A1tica
4.EQUIPO DE TRABAJO No. 4: APLICACIONES EN LA GEOMETRIA. PROBLEMA No. 2 DE LA PAGINA: http://usuarioslycos.es/calculodiferencial/id69.htm
5.http://www.blogger.com.